コレクション サイコロ 3つ 確率 表 278142-サイコロ 3つ 確率 表

5 西尾眞喜子, 樋口保成 確率過程入門(確率論教程シリーズ3) 培風館06 年 6 飛田武幸 ブラウン運動岩波書店1975 年 7 I Karatzas, S E Shreve Brownian motion and stochastic calculus 多くの場合、確率分布を表にまとめた「確率分布表」が用いられる。 例えば、サイコロを振って出る目は \(1\), \(2\), \(3\), \(4\), \(5\), \(6\) のどれかであり、それぞれの目が出る確率は \(\displaystyle \frac{1}{6}\) です。しかし, (3) のように偏りのあるサイコロ投げのエントロピーは硬貨投げのエントロピーより小さく, この意味 で不確実性さが小さいと言える 問題1 次のように出る目にかたよりのあるサイコロ投げを考える Ω = f1;2;3;4;5;6g で確率が

確率 コイン サイコロ くじ 数字カード 計算ドリル 問題集 数学fun

サイコロ 3つ 確率 表

サイコロ 3つ 確率 表-数理統計学まとめ（その3）：第3 章確率変数と確率分布 1 確率変数 サイコロを投げるとき：結果を見るまでは出る目は何かわからない． x1;x2;x3 をそれぞれ1 回目から3 回目までのサイコロを振ったときの 出る目の数とすると，これらが何かはX(表;表;裏) = 2;x(表;表;表;裏) = 3;, である 3) サイコロを1 回投げるという試行に対して出た目の数x は確率変数である 4) サイコロを3 回投げるという試行に対して1 回目に出た目の数x1, 2 回目に出た目の数x2, 3 回目に出

一色パの難しさ パズドラ エクレア牧場

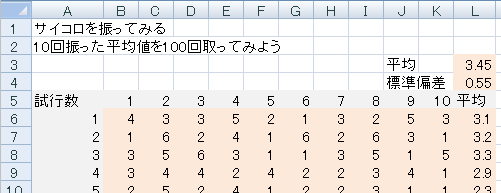
遊：さいころの確率表を作ってみる エクセル関数の使い方 rand()関数とrank（数値,参照,順序）関数の使い方です b列に1、2、3 c列に1～6の数字 セルb3）=b21 セルc3）=int(rand()*6)1 rand()*6で 0～5の数字がランダムで発生します このままでは小数点以下が邪魔なので例3 連続型確率変数X の確率密度関数f(x)が次で与えられるとき，以下の問いに答えよ。 f(x) = cx (0 ≦ x ≦ 1) 0 (その他) (1) cの値を求めよ。(2) P 1 2 ≦ X ≦ 1 を求めよ。 解答(1) ∫ 1 1 f(x)dx = 1より， ∫ 1 0 cxdx = 1が成り立たなければならない。 したがって， ∫ 1 0 cxdx = cx2 21 0 = 1 を解いて，c = 2を得サイコロを繰り返し投げるとき、n 回目に出た目を X n とする。 各X n は 1 ～ 6 の整数値をそれぞれ 1/6 の確率でとり、その期待値は 35 である。 また、確率変数列の平均 X n の値は n → ∞ とすれば 35 に集中する。このことから n が十分大きければ X n はそれぞれの値を等しい比率でとり

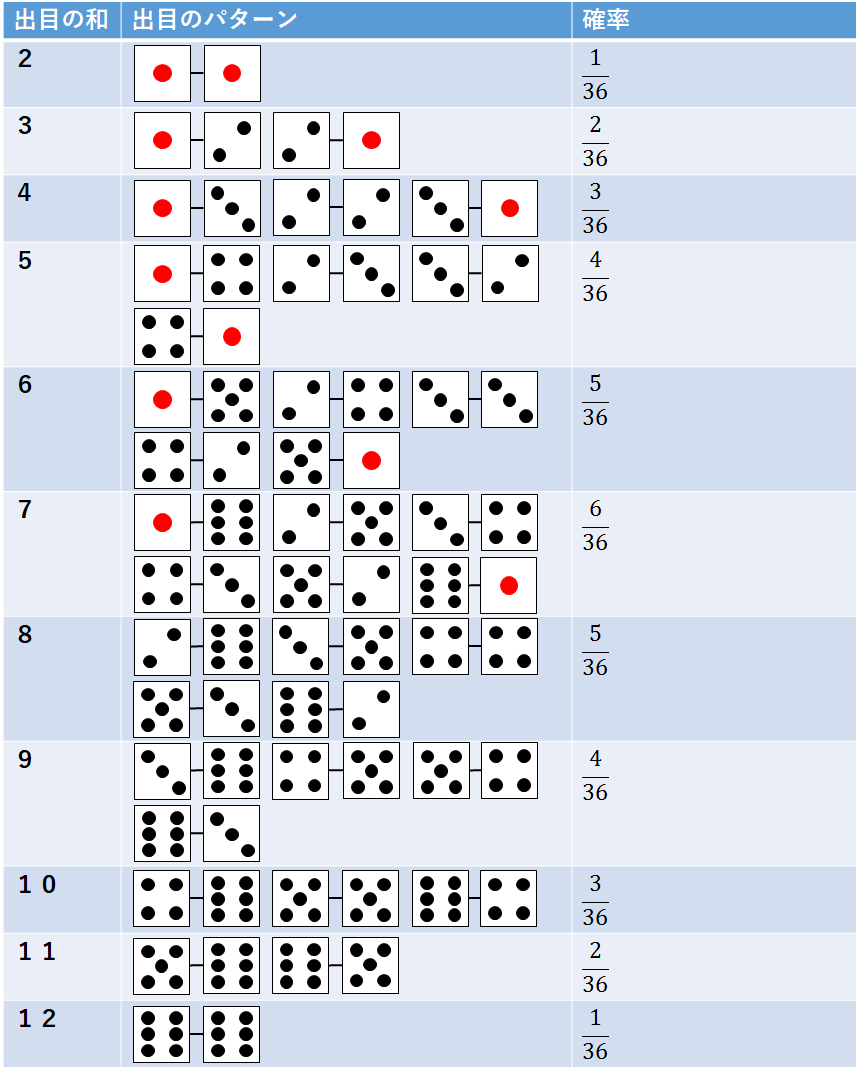
 3標準偏差 4正規分布 5二項分布 6推測統計（t分布、カイ二乗分布） 7仮説検定 と、実務上必要な大体の範囲を押さえている。 たとえば、2項分布の例題として出題されている問題が下の問題だ。 7個のサイコロを振って、150個以上、1が出る確率は？ サイコロの具体例から分かる確率分布の正規近似 Tooda Yuuto 17年6月3日 / 19年9月9日 代わりに使われているのが、無作為に選んだ数百人のデータを集めて「その数百人の代男性の平均身長 \(\overline{X}\)」を「日本全国の代男性の平均身長 \(μ\) の 推定値とる確率が最大になり，確率分布は Fig 2 の ようになります。 0 015 010 005 000 y S2 Fig 2 二つのサイコロを振ったときに出る目の和 S 2 の確率分布 三つのサイコロを振って出る目の和 S 3 は，3 から 18 までの値をとり，確率分布は Fig 3 のように

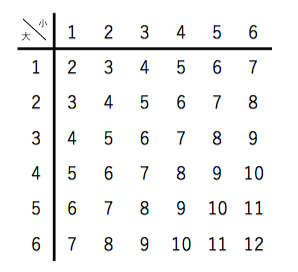
表が6回以上出るときを問われているので 表が6回出るとき、7回出るときをそれぞれ考える必要があります。 q 3つのサイコロの和が3の倍数である確率 3つのサイコロを振ったときの和が3の倍数である確率についてですが、 次の解き方で良いでしょうか？エクセルで表にすると次のような感じです。 では 「サイコロを投げて3の目が出る事象の確率は1/6である」 これを式にしてみましょう。 次のように書くことができます。反復試行の確率が理解できないときは，簡単な具体例で理解すればよい。 x例えば，1 個のサイコロを3 回投げる反復試行において，1 の目が出る回数を とする。 xこのとき， = 2 となるのは，3 回のうち2 回だけ1 の目が出る場合であり，その場合の数

2つのサイコロを振ったとき 出易い合計数はあるか わけいブログ

中学数学の確率の問題の解き方 コイン サイコロ くじ カード 数学fun

サイコロの目の平均の確率分布 0 002 004 006 008 01 012 1 14 18 22 26 3 34 38 42 46 5 54 58 0 001 002 003 004 005 006 007 008 1 13 16 19 22 25 28 31 34 37 4 43 46 49 52 55 58 5 x x 1 x 2 x 5 10 x x 1 x 2 x 10 > @ > @ 5 292 e x 35, v x > @ > @ 10 292 e x 3この 節の初めに取り上げたサイコロ投げを再び考えてみる。 今回は,Xの値にかかわらず , Yの値は2回目のサイコロの出た目の数が{1,2}ならば＝＞y=1, それ以外＝＞y=0 , こうすると,xとyの同時確率は表23サイコロに細工があるかもしれないので、100回投げて平均を計算 確率変数：サイコロの出た目が奇数なら1、偶数なら0 平均： 根元事象の数 n = 6、観測値の数 N = 100 であることに注意！ サイコロの例（5） 21 1回目 2回目 3回目 100回目 サイコロの目 3 6 3 4

確率 コイン サイコロ くじ 数字カード 計算ドリル 問題集 数学fun

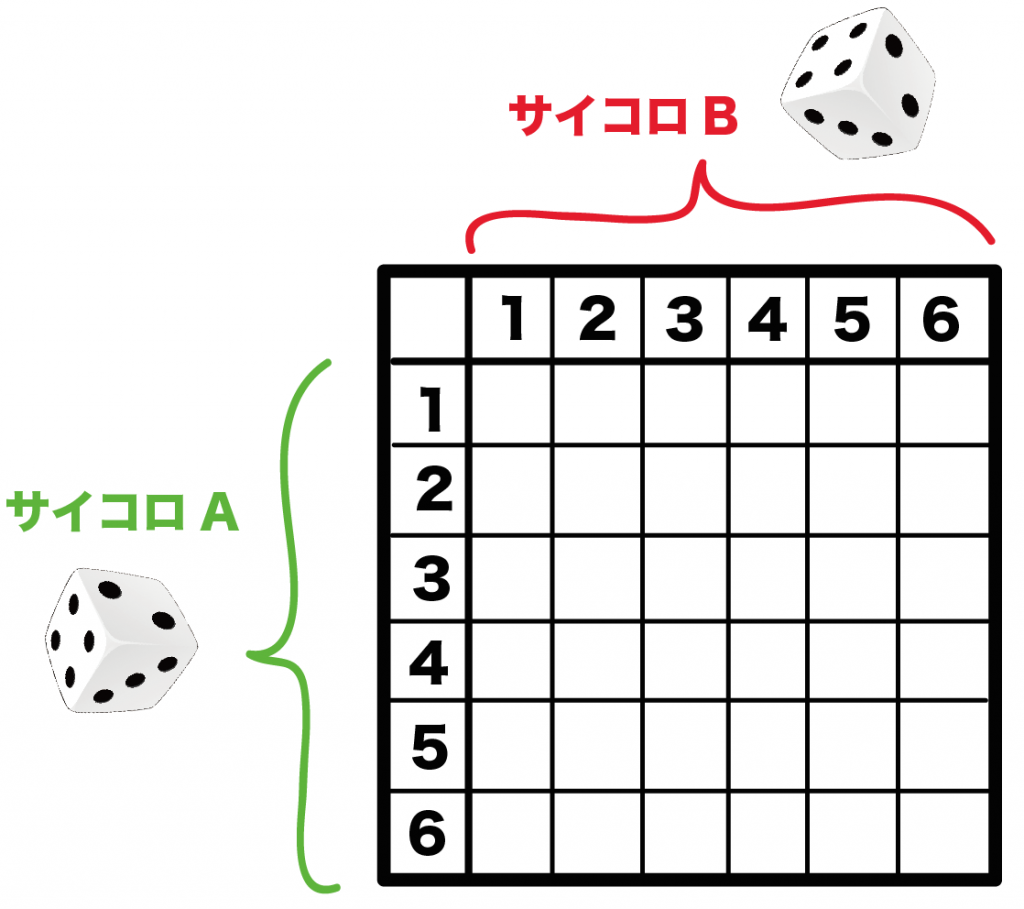
簡単計算 2つのサイコロの確率の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

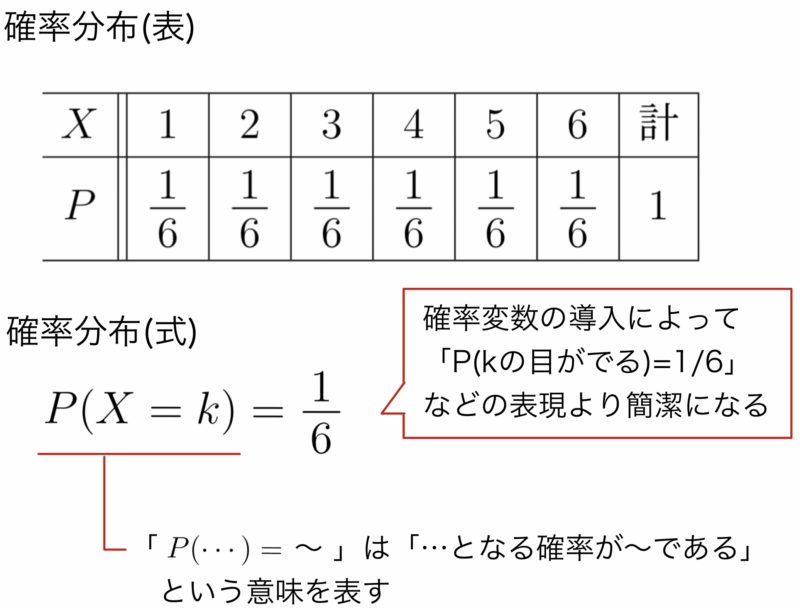
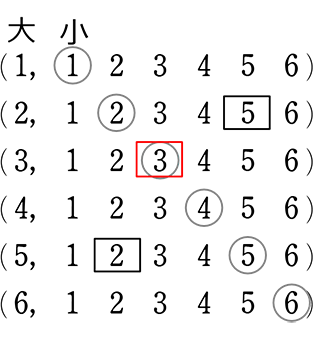
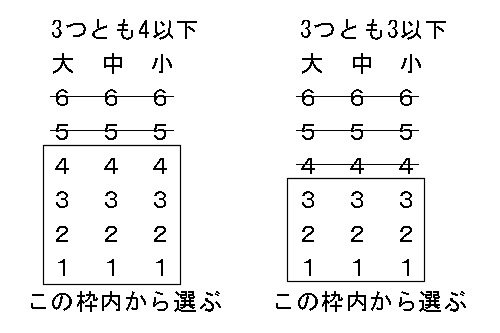
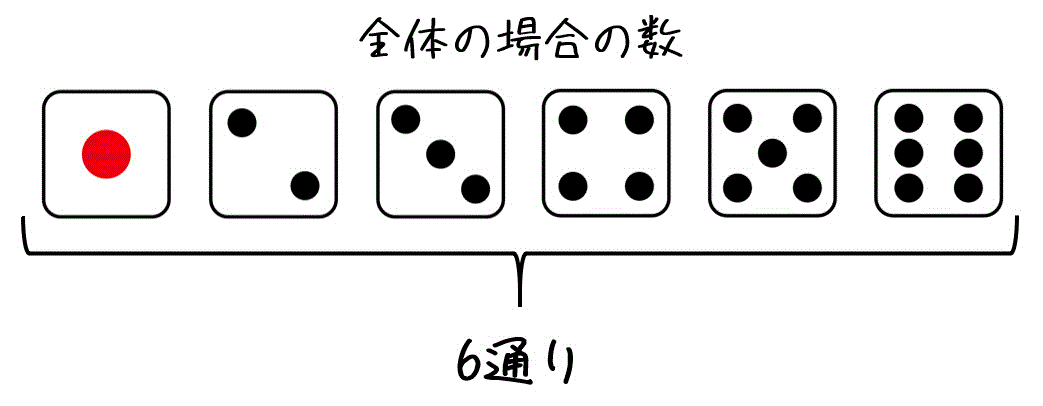
サイコロの目の確率分布 Xを {1,2,3,4,5,6}の値を取る確率変数と定義します。 歪んでいないサイコロの場合、それぞれの目が出る確率は1/6なので、確率分布は以下のようになりますね。 サイコロを振って出る目をXとすると、「確率変数Xは各実現値1,2,3,4,5,6に対してそれぞれ1/6という確率が割り当てられている確率分布に従う」と言います。 と書きます。 このPは英語 確率の問題であれば、表にすべて書くのは216通りあって大変なので、条件に適する組み合わせのみを書き出す手法をおすすめします。 例えば、 (条件) 3つのサイコロの出た目の和が17以上 この場合 (1つ目、2つめ、3つ目)＝ (5,6,6), (6,5,6), (6,6,5), (6,6,6) の 4通り とても簡単な例でしたが、難しくなって数え間違いが心配であれば、 (上の例のように)左側の数字が小さいほう1 理論的な確率分布表に近づいていくはずです。なお，サイコロの{1, 2, 3, 4, 5, 6}の目のように，数字が区切れて並ぶような

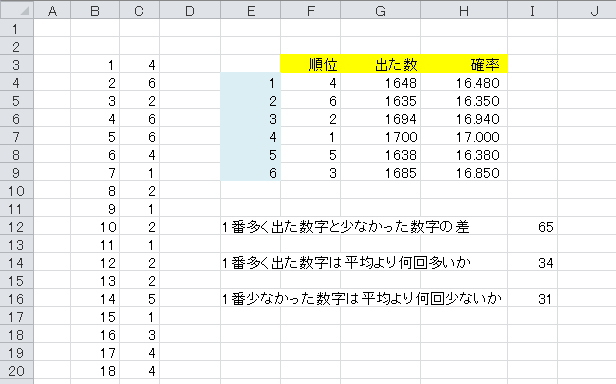
遊 さいころの確率表を作ってみる エクセル関数の使い方

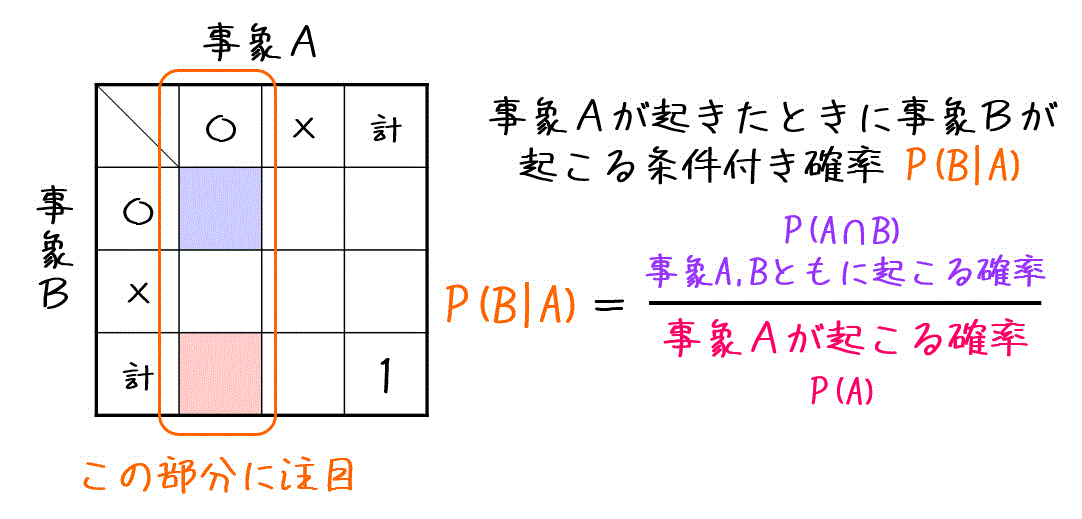
確率 1時間でマスター 覚えておくべき5つの法則 公式 工業大学生ももやまのうさぎ塾

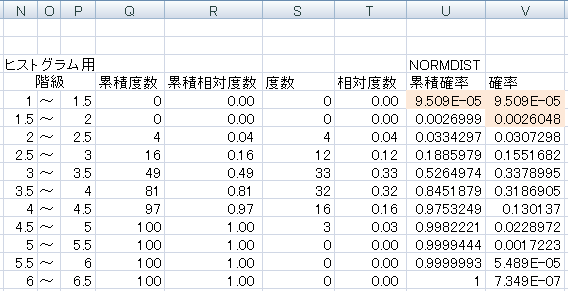
サイコロを n回振って、特定の目 が m回出る確率を計算し表にします。度数分布表とヒストグラムを作る 過去にやったので，詳細は省略。 階級の数は，スタージェスの公式で求めると (log 2 100)1≒8 なので，下の例ではとりあえず1刻みにせず05刻みにして，セル範囲N3T15に作成している。3つのサイコロ pochi3com 場合の数・確率3つのサイコロ 「2つのサイコロを投げたときの目の和が・・・・」という問題は、要は表を作れば解決しますよね。 1 2 3 4 5

２つのサイコロの確率 Youtube

高校数学 数a ２０ 確率 さいころ編part 2 Youtube

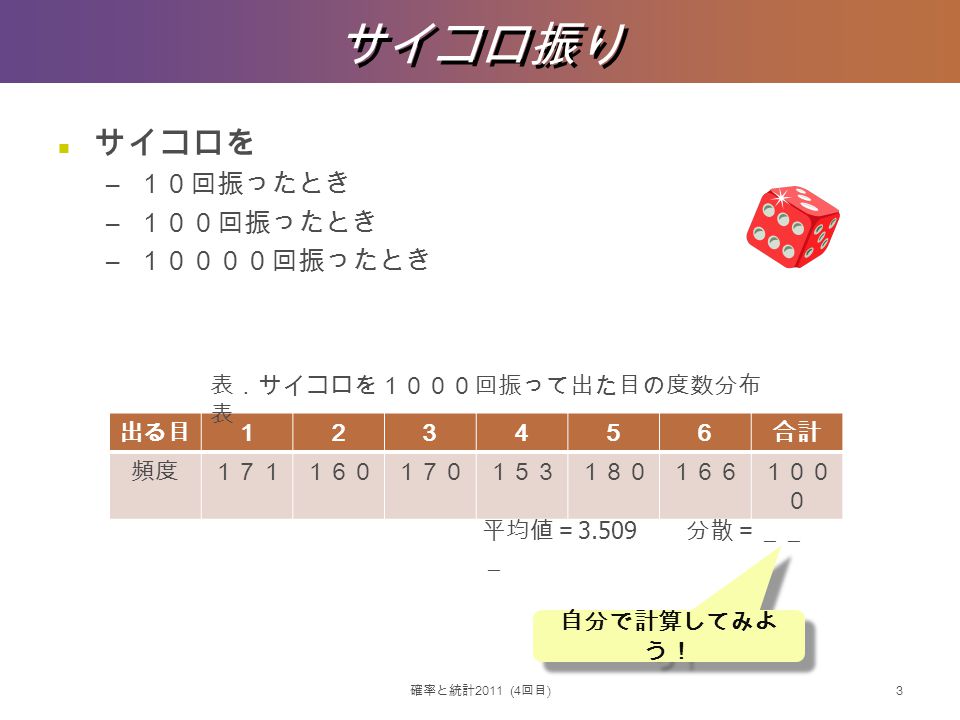
例えば、サイコロを3回振るとき、 「1回目奇数」「2回目偶数」「3回目奇数」 となる確率は、 \( p=\displaystyle \frac{1}{2}\times \displaystyle \frac{1}{2}\times \displaystyle \frac{1}{2}=\displaystyle \frac{1}{8}\) と求めることができるということです。(2) 表が出ればX = 1、裏が出ればX = 0 のようにそれぞ れの起こりうる出来事に0 と1 が対応し、 (3) それぞれの確率が Pr(X = 1) = p, Pr (X = 0) =1 –p, 0 < p < 1 で与えられる確率変数X の分布をベルヌーイ分布という。表32 サイコロを100回投げたときに出た目の度数分布表 サイコロの目 度数 相対度数 累積度数 累積相対度数 1 0 0 2 18 018 38 038 3 10 010 48 048 4 14 014 62 062 5 21 021 0 6 17 017 100 100 合計 100 100 注〆度数は各目が出る確率が等しいという条件で

サイコロを投げて合計するときに何を期待するか

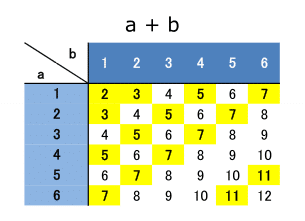
シミュレーション サイコロの出た目の和が素数になる確率 Suika Note

そのおのおのが起こる事象の確率は 1 6 xの値 1 2 3 4 5 6 計 確率 1/6 1/6 1/6 1/6 1/6 1/6 1 (2) x コインを3 回投げて,表の出る回数は0;1;2;3 そのおのおのの確率は次の表のようになる xの値 0 1 2 3 計 確率 1/8 3/8 3台からサイコロを落とす際に、上に向ける面を1から6まで順番に調べる。それぞれ500 回ず つ調べる。 ② 結果と考察 3の面を上にして調べた時は計算上の確率に近づいたが、その他の場合は遠ざかった。どの場 合も計算上の確率になることはなかった。 赤玉が3つ含まれる確率 赤玉が3つ含まれるパターン数は\\begin{align*} {}_4 \mathrm{C} _3 = \frac{ 4 \cdot 3 \cdot 2}{ 1 \cdot 2 \cdot 3} \end{align*}\となり、4通りとなる。 よって、赤玉が3つ含まれる確率は\\frac{4}{} = \frac{1}{5} \となる。 よって、赤玉が2個以上出る確率

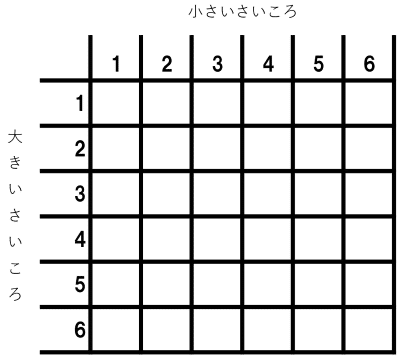
基礎編３ サイコロ２回の分母 大小のさいころ２個 基礎計算研究所 Note

桃鉄のサイコロの出目は狙って操作できるのか というおはなし 怠けるために努力したい

一般に，同時確率分布および周辺分布は，次の表3のような表で表され， P(X=x i, Y=y j)=p ij は同時確率分布を表し， P(X=x i)=p iが X の周辺分布を P(Y=y j)=p ·j が Y の周辺分布を表しています． 周辺分布は， p i·, p ·j のように，ドットを付けて表し， 例えば すなわち，非復元抽出の場合，1回目に赤玉が出る確率は 06 ，白玉が出る確率は 04 だから，2回目を取るときには，全部で 4 個のうちに赤玉が 24 個，白玉が 16 個，3：2の割合で含まれることになり，赤の「濃さ」は変わらない．（元が濃いと出やすいから，取った玉を戻さない場・ 市販のサイコロは3と4が多く、私たちの着目した1が一番少ない。 サイコロを振る回数を重ねると大きくグラフが変化したので、さらに回数を重ねるとど うなるか調べるためにもっと振ってみた。 Ⅲ ① 次に10回まで振ってみた。

反復試行の確率 3つの事象があるときのやり方は 数スタ

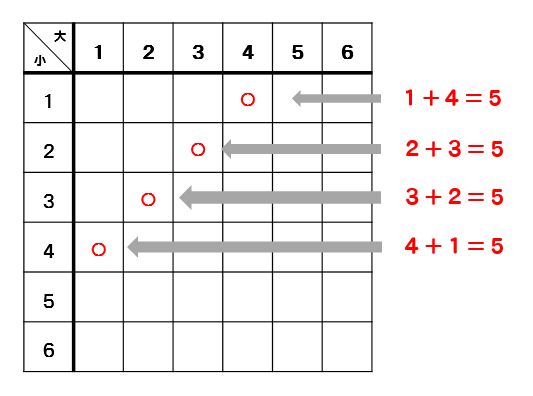
中学数学 さいころ2個の確率問題をパターン別に解説 数スタ

例：サイコロを1つ投げる。 起こりうる結果： 1の目が出る、2の目が出る、、6の目が出る。 確率変数：試行の結果によって値が定まる。 例：サイコロを1つ投げるとき、 x = 1 （もし出目が偶数なら）；0（それ以外のとき） x = （出目の2倍） 3 Apictnyohddm7 サイコロ 3つ 確率 表 サイコロ 3つ 確率 表すなわち，非復元抽出の場合，1回目に赤玉が出る確率は 06 ，白玉が出る確率は 04 だから，2回目を取るときには，全部で 4 個のうちに赤玉が 24 個，白玉が 16 個，3：2の割合で含まれることになり，赤の「濃さ」は変わらない．（元が濃いと出やすいから，取った玉を戻さない場合でも濃さは変

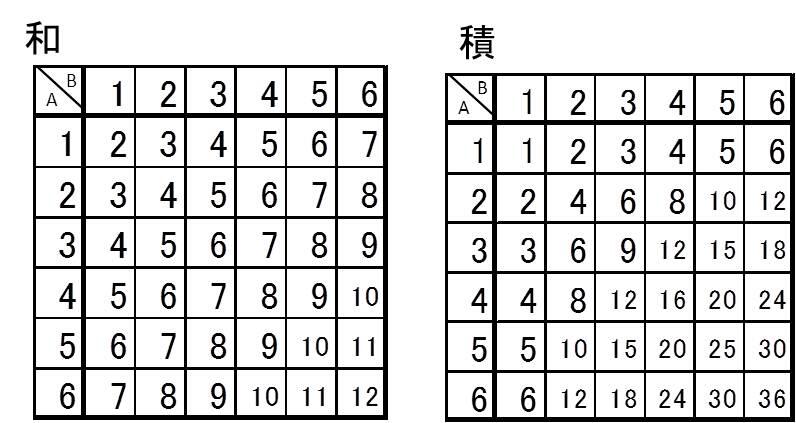
140字で高校受験 数学 確率 2つのサイコロの問題は表を書く 和を使う問題なら和の表 積を使う問題なら積の表 高校受験 数学 確率 T Co 6uhhpix2up

無料 中２数学 基本問題 問題プリント 236 確率４ 求め方２

漸化式の応用 確率漸化式 おいしい数学

バックギャモンでサイコロ２つの出目の確率を知って有利に戦う

2

サイコロ 2つの確率問題は なぜ 分母が 36になるんですか 6 6で12 Clearnote

Naop Jp

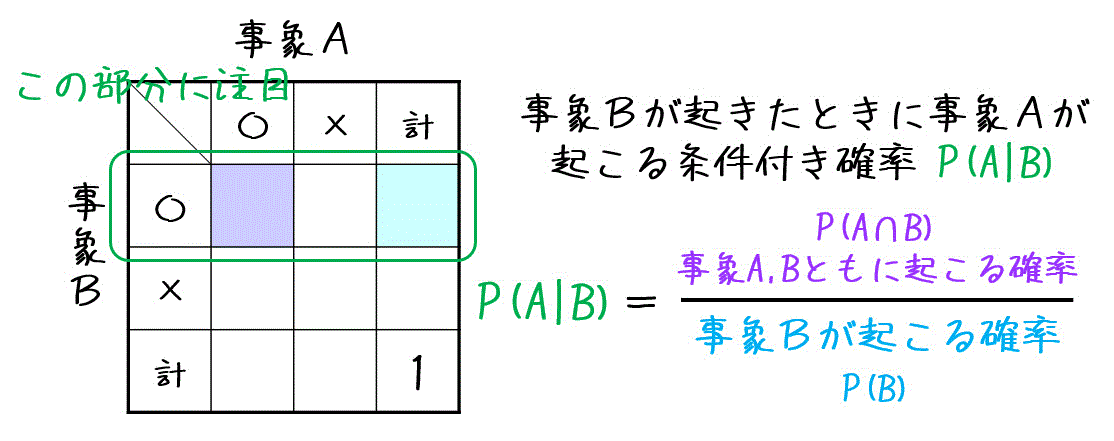
確率 1時間でマスター 覚えておくべき5つの法則 公式 工業大学生ももやまのうさぎ塾

確率の基本 サイコロを投げる 苦手な数学を簡単に

中学数学の確率 コインとサイコロの問題の解き方と樹形図 リョースケ大学

さいころをふってみた Kec近畿予備校 Kec近畿教育学院 公式ブログ

応用情報処理 第5回 連続確率分布 Excelサイコロ

後編 サイコロ3つのうち1 2個の出目を当てる 大小 シックボー の確率と配当まとめ カジラグ

13 Introduction To Experimental Mathematics Ii By D Furihata

技術解説 マルコフモデルと隠れマルコフモデル ミエルカai は 自然言語処理技術を中心とした Rpa開発 サイト改善 流入改善レコメンドエンジンを開発

解る説明と実戦向けのコツ

確率の練習問題 数学の要点まとめ 練習問題一覧

確率の解き方 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導

シチャーマンのサイコロ Wikipedia

確率の独立性の解説 積の期待値 和の分散 具体例 理数アラカルト

確率の問題で質問なんですが 大小２つのサイコロを振ります Clearnote

応用情報処理 第5回 連続確率分布 Excelサイコロ

一色パの難しさ パズドラ エクレア牧場

サイコロ３個を振った時の確立について質問です サイコロ３個を振っ 数学 教えて Goo

確率変数と確率分布の基本 さいころの例と確率分布のいろいろな例 Irohabook

1

確率の問題の解き方 さいころ 3 現役塾講師のわかりやすい中学数学の解き方

2

サイコロ10コの出目の合計を当てろ やぐち建築士の備忘録

どうしてサイコロを別のものとして考えるのに 3 3 は Yahoo 知恵袋

すごろくでサイコロを何回振ればゴールできるか サイコロが2個の場合

中学数学 3つのサイコロの確率の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

確率変数 統計ブログ

高校入試確率の傾向と対策 定番問題はマスターしよう 高校入試徹底対策ガイド

2

数学aの問題なんですけど さいころの確率の問題のときなぜ分母が36になるの Yahoo 知恵袋

3つのサイコロを振って1 2 3が出る確率と1 1 １が出る確率って同じ Yahoo 知恵袋

１３ 少なくとも の確率 葛藤のブログ

確率 シンプルなもの チーム エン

中学 数学 確率 解き方 サイコロ

独立な試行 による事象 の確率 数学が嫌いなんです

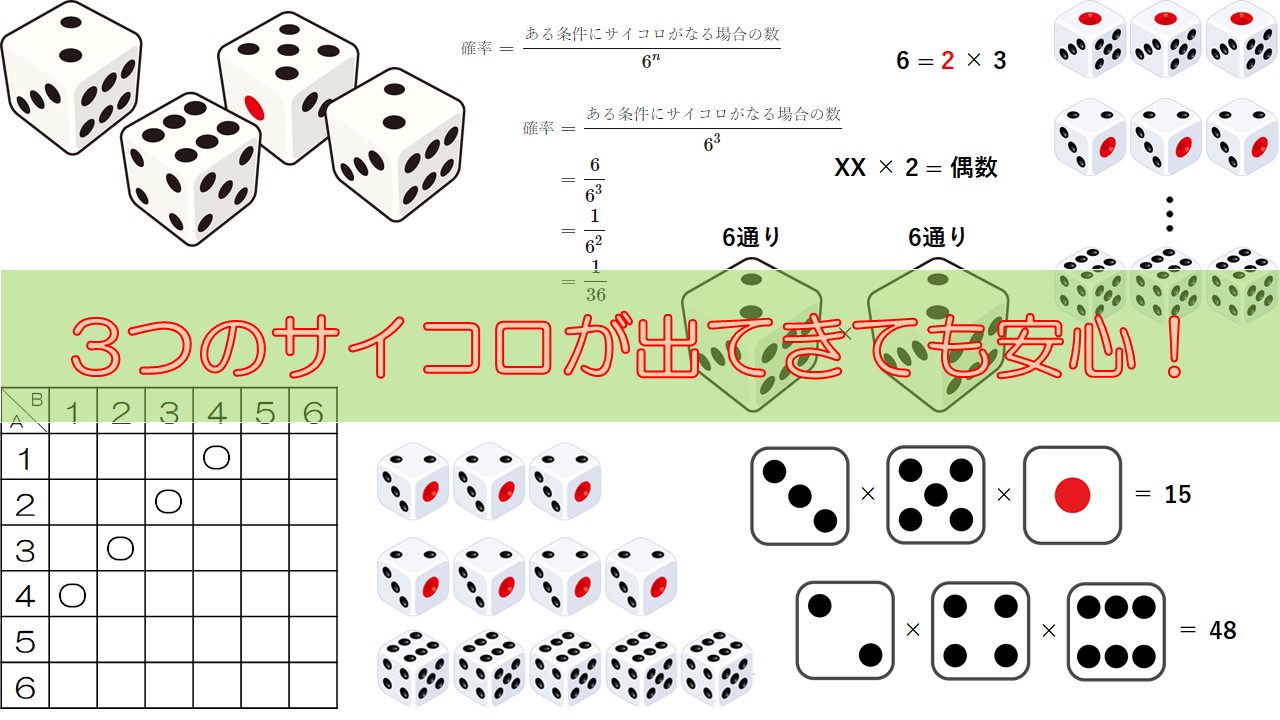
中学2年数学 確率 3つ以上のサイコロが出てくる確率の問題を攻略しよう 数学の面白いこと 役に立つことをまとめたサイト

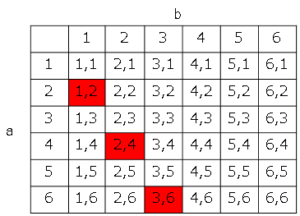
サイコロとグラフの関係 数学の要点まとめ 練習問題一覧

問題演習 確率

期待値 の 確実な解き方

9 5 確率と独立 統計学の時間 統計web

前編 出目の組み合わせから考える 大小 シックボー 賭け方別の確率と配当まとめ カジラグ

中学数学 3つのサイコロの確率の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

1

地道に数える方が早いことも 中２の確率 立ち読み計算ドリル ききょうけん キッズの教養を考える研究室

03 号 ３２面体サイコロ Astamuse

1

確率の独立性の解説 積の期待値 和の分散 具体例 理数アラカルト

大小2個のさいころを同時に投げるとき目の和が6の倍数になる確率を求めよ Clearnote

３つのサイコロ

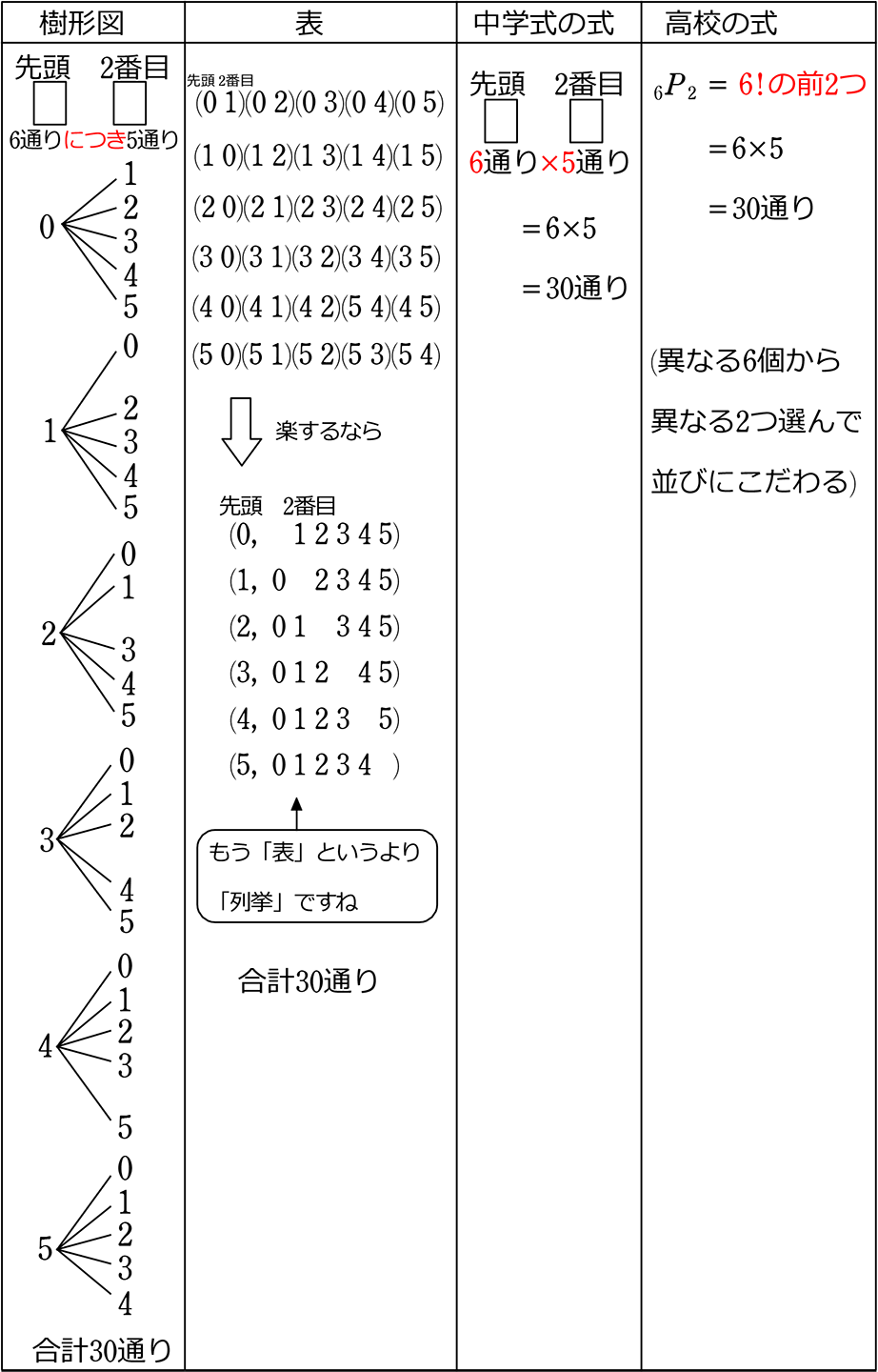
中学数学 場合の数

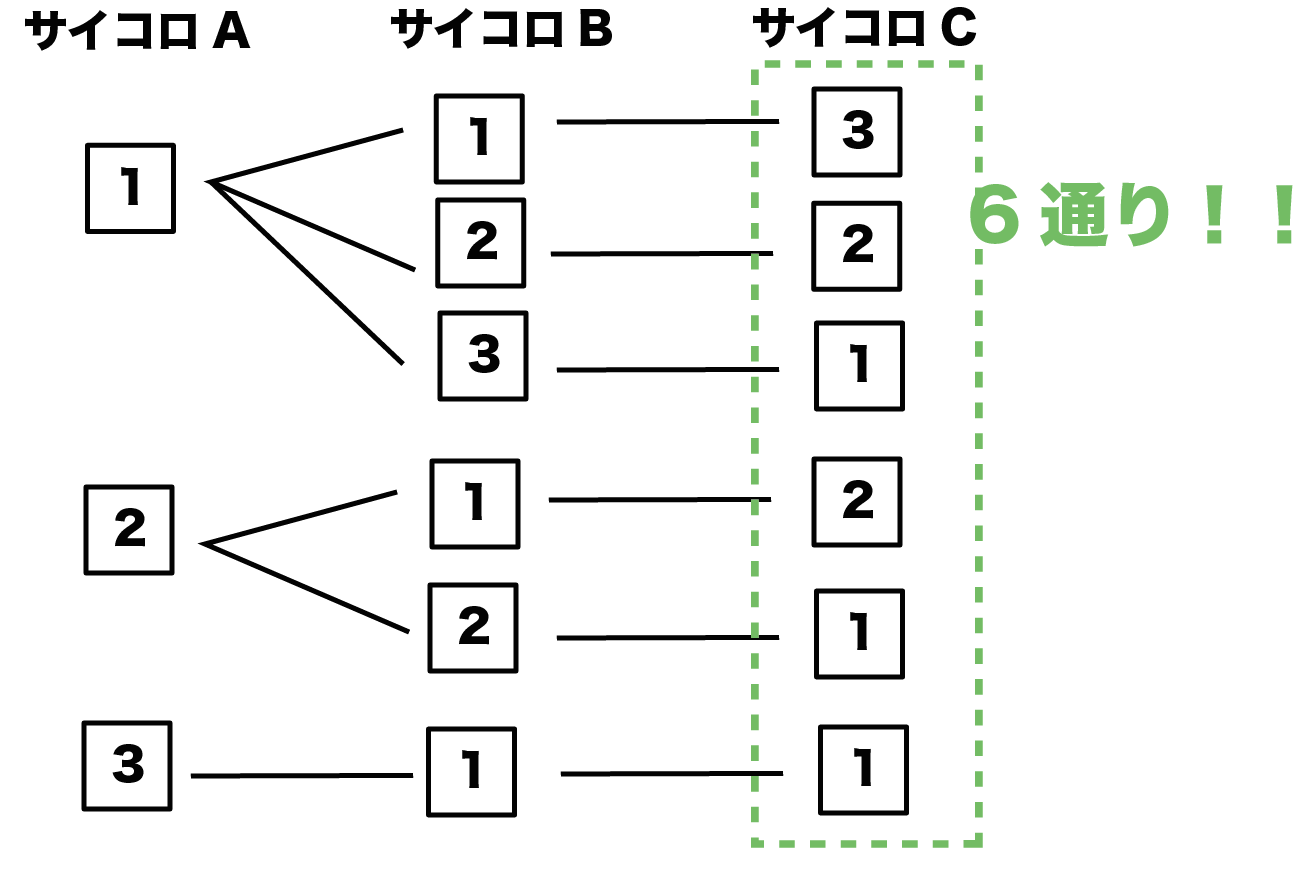
中学数学 3つのサイコロの確率の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

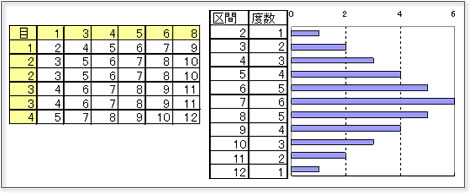
株 日科技研 第44話 シッチャーマンのサイコロ 六一学者の千字一話 会員広場

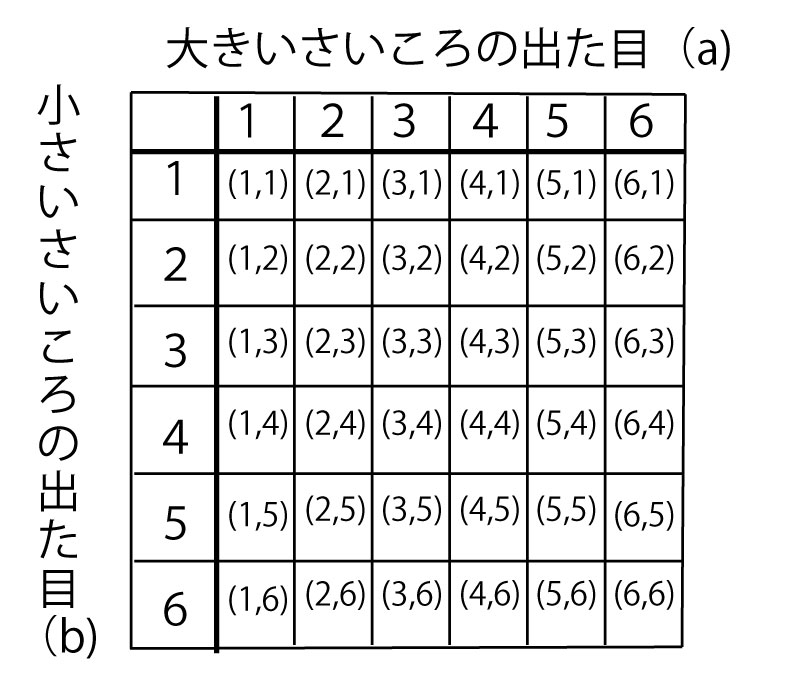
16年前期 千葉県公立高校入試 数学 第2問 4 確率 解答 解説 船橋市議会議員 朝倉幹晴公式サイト

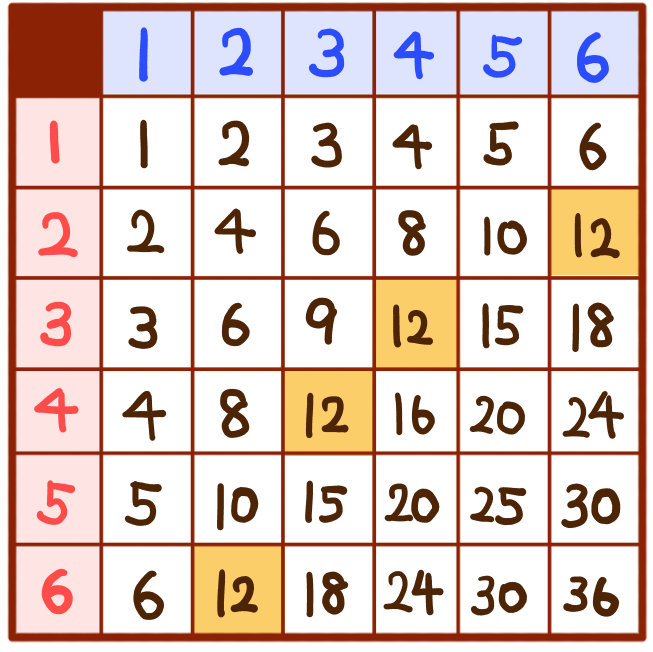
サイコロの確率の練習問題 高校入試 中学数学 を難問まで難易度別に解説 坂田先生のブログ

中2数学 2つのサイコロを投げるときに樹形図描く奴wwwwwwwwww 確率 牛乳屋黄三郎の雑感ブログ

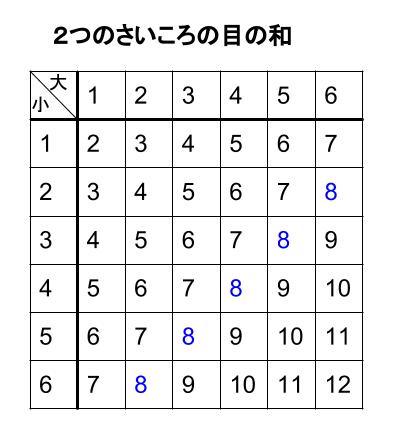
中学数学 確率 さいころ 中学数学の無料オンライン学習サイトchu Su

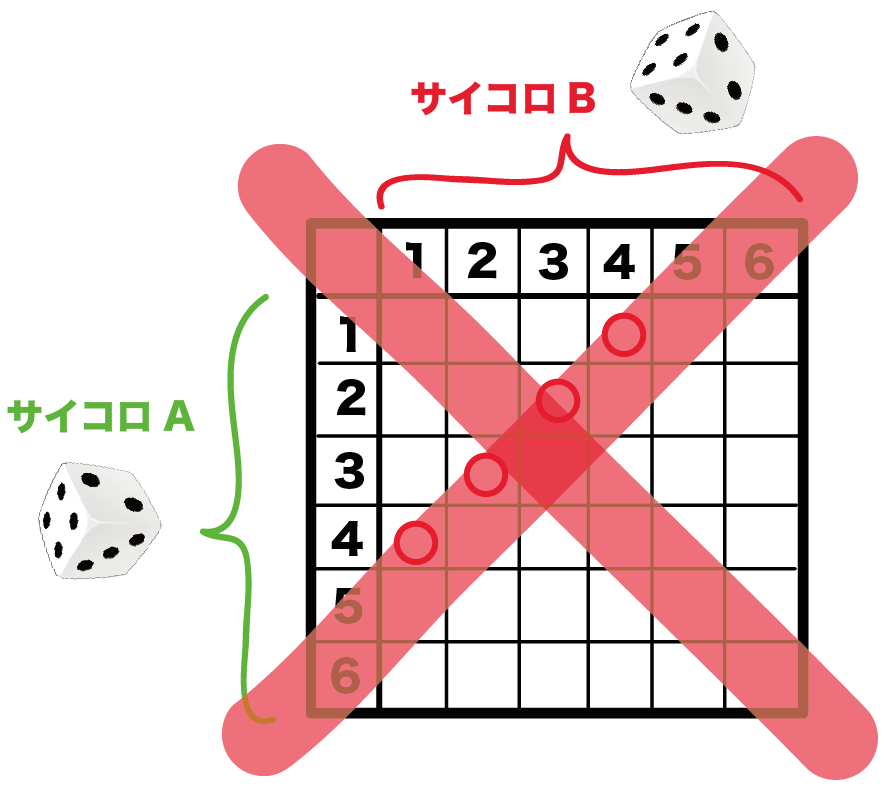
中学数学 3つのサイコロの確率の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

確率とは 公式 計算式の立て方と確率の求め方 受験辞典

中学数学 確率

確率 1時間でマスター 覚えておくべき5つの法則 公式 工業大学生ももやまのうさぎ塾

確率と統計 確率編 平成23年10月13日 木 Ppt Video Online Download

2

1

サイコロを２つまたは３つ以上振る確率の求め方と重複試行

二つのサイコロを転がす確率 二つのサイコロのサンプルスペース 例 Tombouctou

確率 1時間でマスター 覚えておくべき5つの法則 公式 工業大学生ももやまのうさぎ塾

Nyuzenn J El Tym Ed Jp

2

2

2

確率の計算ができないキミへ 数学a スタディクラブ情報局

やさしい確率の解き方 全学年 数学 公式 家庭教師のアルファ プロ講師による高品質指導

期待値とは 計算公式と求め方をわかりやすく解説 受験辞典

さいころを2個同時に振ったとき 8なる確立 立方体のさいころを2個同 数学 教えて Goo

確率の計算ができないキミへ 数学a スタディクラブ情報局

サイコロの目は予想できる 岡山モノポリークラブ

サイコロの確率の計算問題１３選 ２つ投げる場合の求め方とは 遊ぶ数学

中2数学 さいころの確率の解き方と練習問題

大小2つのさいころを同時に投げた時 目の和が4の倍数になるのは何通り 数学 教えて Goo

確率の問題の解き方 ２つを取り出す 現役塾講師のわかりやすい中学数学の解き方

2個のサイコロの区別 2個のサイコロを投げる時 出る目が2と1になる確率 Okwave

中学数学 3つのサイコロの確率の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

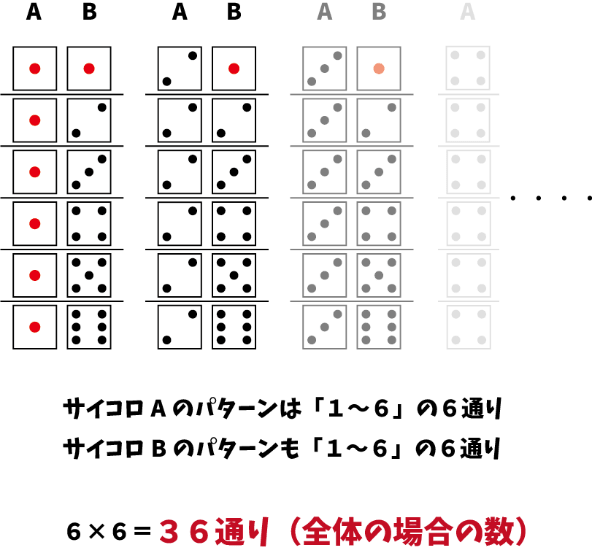
中学数学 確率問題の解き方 サイコロ トランプ カード 硬貨 玉を取り出す

大小2個のサイコロを同時に投げ 少なくとも一方の目が3の倍数 Yahoo 知恵袋

Incoming Term: サイコロ 3つ 確率 表,